C언어로 쉽게 풀어쓴 자료구조: 9장 우선순위 큐
9.1 우선순위 큐 추상 데이터 타입
우선순위 큐의 소개
- 데이터들이 우선순위를 가지고 있고 우선 순위가 높은 데이터가 먼저 나가게 된다.
| 자료구조 | 삭제되는 요소 |
| 스택 | 가장 최근에 들어온 데이터 |
| 큐 | 가장 먼저 들어온 데이터 |
| 우선순위 쿠 | 가장 우선순위가 높은 데이터 |
우선순위 큐 추상자료형
- 기본적으로 다른 자료구조와 같다.
- delete 연산 시 가장 우선 순위가 높은 요소를 삭제하고 이 요소를 반환한다.
9.2 우선순위 큐의 구현 방법
1. 배열
- 정렬되지 않은 배열
- 요소 삽입: 배열의 맨 끝에 새로운 요소를 추가한다.
- 요소 삭제: 처음부터 끝까지 모든 요소들을 스캔해야 한다. 삭제 후 뒤의 요소를 앞으로 이동시켜야 한다.
- 정렬된 배열
- 요소 삽입: 순차 탐색, 이진탐색등을 사용하여 다른 요소와 비교하여 위치를 찾은 후, 삽입 위치 뒤에 있는 요소들을 이동시켜 빈 자리를 만든 후 삽입
- 요소 삭제: 배열의 인덱스가 높은것이 우선순위가 높다고 가정하면, 인덱스가 큰 요소를 삭제한다.
2. 연결리스트
- 정렬되지 않은 연결리스트
- 요소 삽입: 첫 번째 노드로 삽입, 배열과 달리 다른 노드를 이동시키지 않고, 포인터만 변경한다.
- 요소 삭제: 포인터를 따라 모든 노드를 스캔한다.
- 정렬된 연결리스트
- 요소 삽입: 우선순위가 높은 요소가 첫 번째 노드가 되도록 한다.
- 요소 삭제: 첫 번째 노드를 삭제한다.
3. 힙(Heap)
- 느슨한 정렬 상태 유지(완전히 정렬 된 것도 아니고, 전혀 정렬 안된 상태도 아닌 상태)
9.3 힙(Heap)
- 완전이진트리 기반의 "더미"와 모습이 비슷한 특정한 자료 구조
- 중복된 값을 허용한다.
- 느슨한 정렬 산태를 유지한다.
- 여러 개의 값들 중 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료 구조
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리
※완전이진트리?
: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
힙의 종류
- 최대 힙(max heap): 부모 노드의 키 값 > 자식 노드 키 값
- 최소 힙(min heap): 부모 노드의 키 값 < 자식 노드 키 값
힙 구현
- 배열의 첫 번째 인덱스 0은 사용하지 않는다.
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스)/2
9.4 힙의 구현
힙의 정의
#define MAX_ELEMENT 200
typedef struct {
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
삽입 연산(최대힙)
- 힙에 새로운 요소 추가
- 새로운 노드를 힙의 마지막 노드로 삽입
- 부모노드와 비교
- 부모 노드 < 자식 노드 ➡️ 서로 교환
- 부모 노드 > 자식 노드 ➡️ 더 이상 교환하지 않는다.
// 삽입 함수
void insert_max_heap(HeapType* h, element item)
{
int i;
i = ++(h->heap_size);
// 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정
while ((i != 1) && (item.key > h->heap[i / 2].key)) {
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item; // 새로운 노드를 삽입
}
삭제 연산(최대힙)
- 최대 힙에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
- 최대힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
- 삭제 후 힙을 재구성
- 재구성 과정
- 루트 노드 삭제
- 빈 루트 노드 자리에 힙의 마지막 노드를 가져온다.
- 새로운 루트 노드와 자식 노드를 비교하여 위치를 교환한다.
- 교환이 일어나지 않을때까지 반복한다.
- 재구성 과정
// 삭제 함수
element delete_max_heap(HeapType* h)
{
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while (child <= h->heap_size) {
// 현재 노드의 자식노드 중 더 작은 자식노드를 찾는다.
if ((child < h->heap_size) &&
(h->heap[child].key) < h->heap[child + 1].key)
child++;
if (temp.key >= h->heap[child].key) break;
// 한 단계 아래로 이동
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}
9.5 힙 정렬
- 정렬되지 않은 데이터를 차례로 최대힙에 추가한다.
- 한 번에 하나씩 요소를 힙에서 꺼내어 배열의 뒤쪽부터 저장한다.
void heap_sort(element a[], int n) {
int i;
HeapType* h;
// 힙 생성
h = create();
// 힙 초기화
init(h);
// 주어진 배열의 모든 요소를 최대 힙에 삽입
for (i = 0; i < n; i++) {
insert_max_heap(h, a[i]);
}
// 최대 힙에서 하나씩 요소를 꺼내 배열에 역순으로 저장
for (i = (n - 1); i >= 0; i--) {
a[i] = delete_max_heap(h);
}
// 힙 메모리 해제
free(h);
}
9.6 머신 스케줄링(Machine Schedling)
- 모든 기계를 가동하여 가장 최소의 시간 안에 작업들을 모두 끝내는 것
- LPT(Longest Pro-ceccing Time first)
- 가장 긴 작업을 우선적으로 기계에 할당
- 각 작업들을 가장 먼저 사용가능하게 되는 기계에 할당
- 최소힙을 사용

9.7 허프만 코드(Huffman)
- 데이터를 압축하는 방법
- 문자의 빈도수에 따라 다른 비트열을 만들어 압축하는 알고리즘
허프만 코드 생성 단계
1. 문자의 빈도수
Characters: {A, B, C, D, E}
Frequencies: {5, 9, 12, 13, 16}
2. 우선순위 큐(또는 최소 힙) 초기화
- 각 요소가 다음을 포함하는 노드인 우선순위 대기열을 만든다.
- 문자(또는 문자 그룹)
- 빈도(우선순위 대기열에서 정렬 키로 사용됨)
3. 허프만 트리 구축
- 우선순위 대기열의 가장 작은 두 노드를 새 노드로 반복적으로 결합합니다.
- 대기열에서 빈도가 가장 작은 두 개의 노드를 제거합니다.
- 다음 두 노드를 결합하는 새 노드를 만듭니다.
- 해당 주파수의 합을 새 노드의 주파수로 할당합니다.
- 두 노드를 새 노드의 자식으로 만듭니다(하나는 왼쪽 자식이 되고 다른 하나는 오른쪽 자식이 됨).
- 이 새 노드를 우선순위 대기열에 다시 삽입합니다.
- 대기열에 허프만 트리의 루트가 되는 노드가 하나만 남을 때까지 반복.
트리 작성의 예:
주어진 주파수 {A=5, B=9, C=12, D=13, E=16}:
- A(5)와 B(9)를 결합 → New Node AB(14).
- C(12)와 AB(14) → New Node CAB(26)을 결합합니다.
- D(13)과 E(16)를 결합 → New Node DE(29).
- CAB(26)과 DE(29) → 루트 노드(55)를 결합합니다.
55
/ \
26 29
/ \ / \
12 14 13 16
/ \
5 9
4. 바이너리 코드 할당
- 허프만 트리를 탐색하여 각 문자에 이진 코드를 할당.
- 왼쪽 간선: 비트 1
- 오른쪽 간선: 비트 0
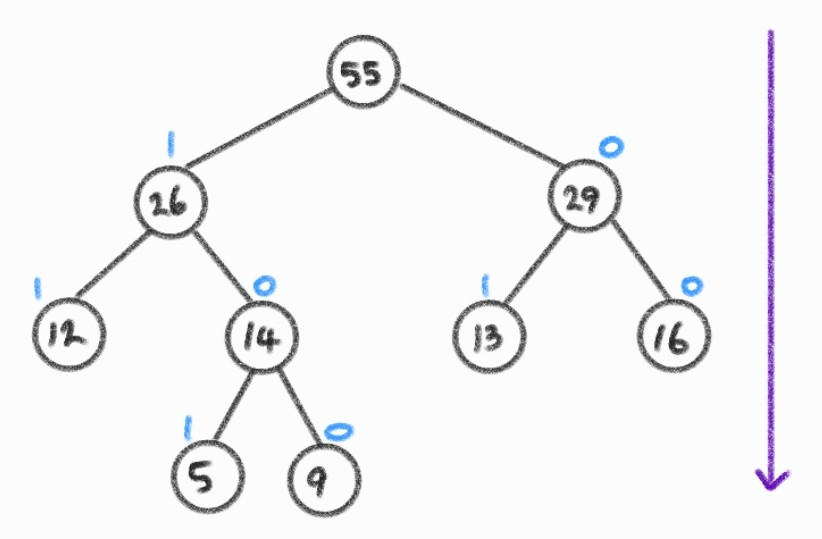
- 리프 노드(문자)는 최종 바이너리 코드를 얻는다.
A: 101
B: 100
C: 11
D: 01
E: 00
허프만 코드 프로그램
void huffman_tree(int freq[], char ch_list[], int n) {
int i;
TreeNode *node, *x; // 트리 노드와 임시 노드 포인터 선언
HeapType* heap; // 최소 힙 포인터 선언
element e, e1, e2; // 힙의 요소를 저장할 구조체 선언
int codes[100]; // 코드를 저장할 배열 선언
int top = 0; // 스택 포인터 역할을 하는 변수
heap = create(); // 힙 생성
init(heap); // 힙 초기화
// 각 문자에 대해 노드를 생성하고 최소 힙에 삽입
for (i = 0; i < n; i++) {
node = make_tree(NULL, NULL); // 새 트리 노드 생성
e.ch = node->ch = ch_list[i]; // 노드에 문자 할당
e.key = node->weight = freq[i]; // 노드에 빈도(가중치) 할당
e.ptree = node; // 힙 요소에 노드 포인터 연결
insert_min_heap(heap, e); // 최소 힙에 삽입
}
// 허프만 트리 생성 과정
for (i = 1; i < n; i++) {
e1 = delete_min_heap(heap); // 최소 힙에서 가장 작은 노드 꺼냄
e2 = delete_min_heap(heap); // 최소 힙에서 두 번째로 작은 노드 꺼냄
x = make_tree(e1.ptree, e2.ptree); // 두 노드를 합쳐 새 트리 노드 생성
e.key = x->weight = e1.key + e2.key; // 새로운 노드의 가중치는 두 노드 가중치의 합
e.ptree = x; // 새로운 노드 포인터 설정
printf("%d+%d->%d \n", e1.key, e2.key, e.key); // 트리 합성 과정 출력
insert_min_heap(heap, e); // 새로 생성된 노드를 최소 힙에 삽입
}
e = delete_min_heap(heap); // 최종 허프만 트리 루트를 꺼냄
print_codes(e.ptree, codes, top); // 트리를 순회하며 허프만 코드 출력
destroy_tree(e.ptree); // 트리 메모리 해제
free(heap); // 힙 메모리 해제
}
'C언어로 쉽게 풀어쓴 자료구조' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 11장 그래프 Ⅱ (2) | 2025.01.30 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 10장 그래프 Ⅰ (1) | 2025.01.14 |
| [C언어로 쉽게 풀어쓴 자료구조] 8장 트리 - Ⅱ (0) | 2024.12.12 |
| [C언어로 쉽게 풀어쓴 자료구조] 8장 트리 - Ⅰ (2) | 2024.11.24 |
| [C언어로 쉽게 풀어쓴 자료구조] 7장 연결리스트 - Ⅱ (1) | 2024.11.23 |